Normalize的作用

normalize的最主要的一个作用是将数据中的不同的特征缩放到同一个量纲上（或者可以说无量纲化）。比如果说有一个特征值的范围是[0,1]另一个特征的范围是[0,1000],那么优化算法（尤其是基于梯度的优化方法）在更新的时候尤其会重视特征值大的特征，而忽视特征值小的特征。为了避免这个问题就需要normalization了，把所有的特征放在一个量纲上。

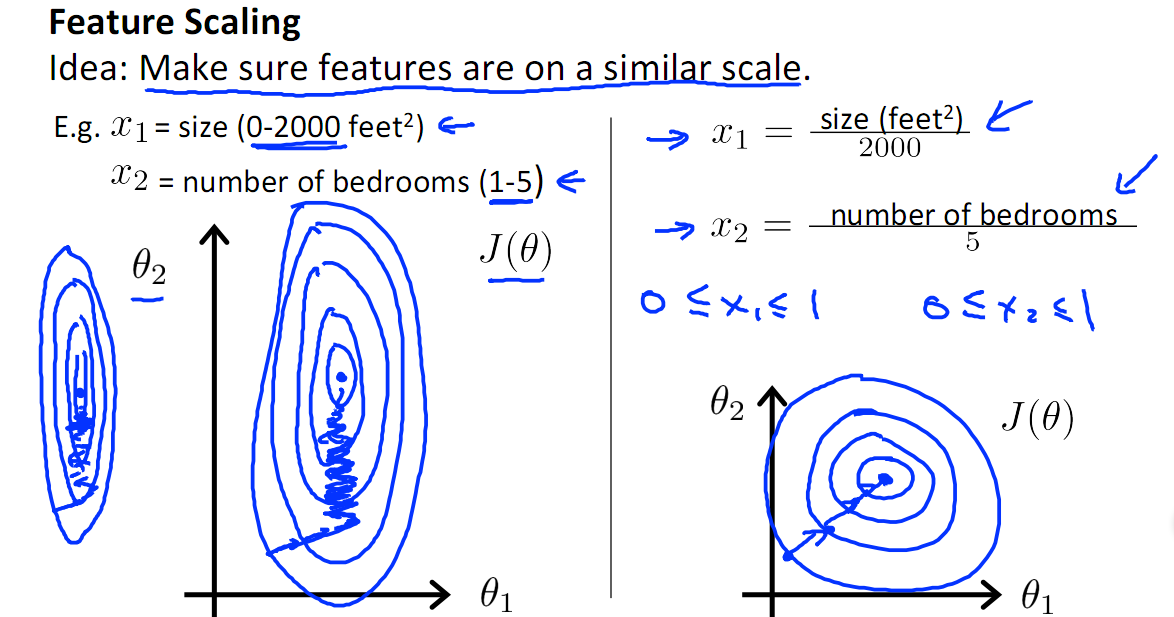
常用的normalization的方法

主要有两种方法，min-max normalization 和 Z-score normalization。

min-max normalization

$$x_{minmax} = \frac{x - x_{min}}{x_{max} - x_{min}}$$

主要有两个缺陷:

1. 新加入的数据会导致$x_{max}$和$x_{min}$ 会发生变化，需要重新定义
2. 异常值会极大地影响minmax的表现
3. minmax不适用于长尾分布

比较适合于min和max固定的任务，比如图像像素归一化。

Z-score normalization

$$x_{zscore} = \frac{x - min(x)}{stdev(x)}$$

z-score的问题没有min-max多，对异常值也较为鲁棒性。且经过处理的数据会较为贴近正态分布（不是变为），大多数的数据会聚集在0附近，方差为1.

Caveat: it is a common misconception that standardized scores such as z-scores alter the shape of a distribution; in particular, be aware that a z*-scores cannot magically make a non-normal variable normal.

其他的还有logistic，lognormal，TanH等，见

Normalizing

和上面不同的方式，是直接对样本进行单位化，即

$$x = \frac{x}{norm(x)}$$

不同的norm会有不同的结果，常见的是L2 norm